5.3. PROPIEDADES Y TEOREMAS DE LOS POLÍGONOS

Teorema 1: La suma de los ángulos interiores de un polígono es igual a 180° por (n – 2), donde n es el número de lados del polígono. Cuando hablamos de un polígono regular, el valor de cada uno sus ángulos es el mismo, y es igual a la división de la suma de sus ángulos interiores entre su número de lados (n):

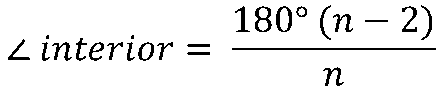
EJEMPLO: Calcular la medida del ángulo interior de un pentágono regular.

Solución: un pentágono tiene 5 lados (n=5), por lo cual sustituimos en la fórmula:

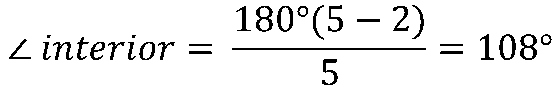
Teorema 2: La suma de los ángulos exteriores de un polígono es igual a 360°.

FIGURA 5: Ángulos exteriores de un polígono

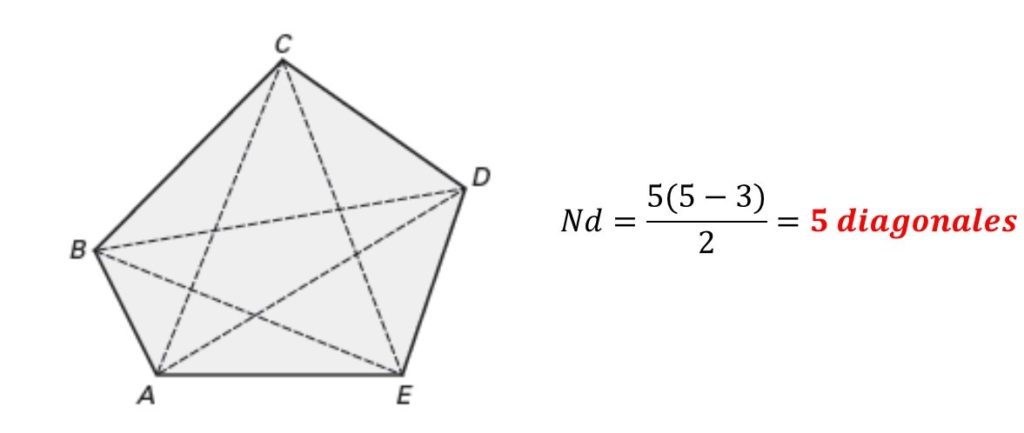
Teorema 3: El número total de diagonales (Nd) de un polígono es igual a:

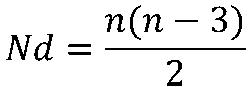
Donde n es el número de lados del polígono

5.4 PERÍMETRO Y ÁREA DE UN POLÍGONO

El perímetro de un polígono se calcula sumando la longitud de cada uno de sus lados. El área de un polígono regular es igual al semiperímetro (SP) multiplicado por su apotema. El semiperímetro de una figura es la mitad del perímetro total.

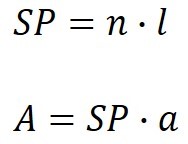
Donde n es el número de lados del polígono, l es la longitud de un lado, SP es el semiperímetro y a es su apotema.

5.5 CUADRILATEROS

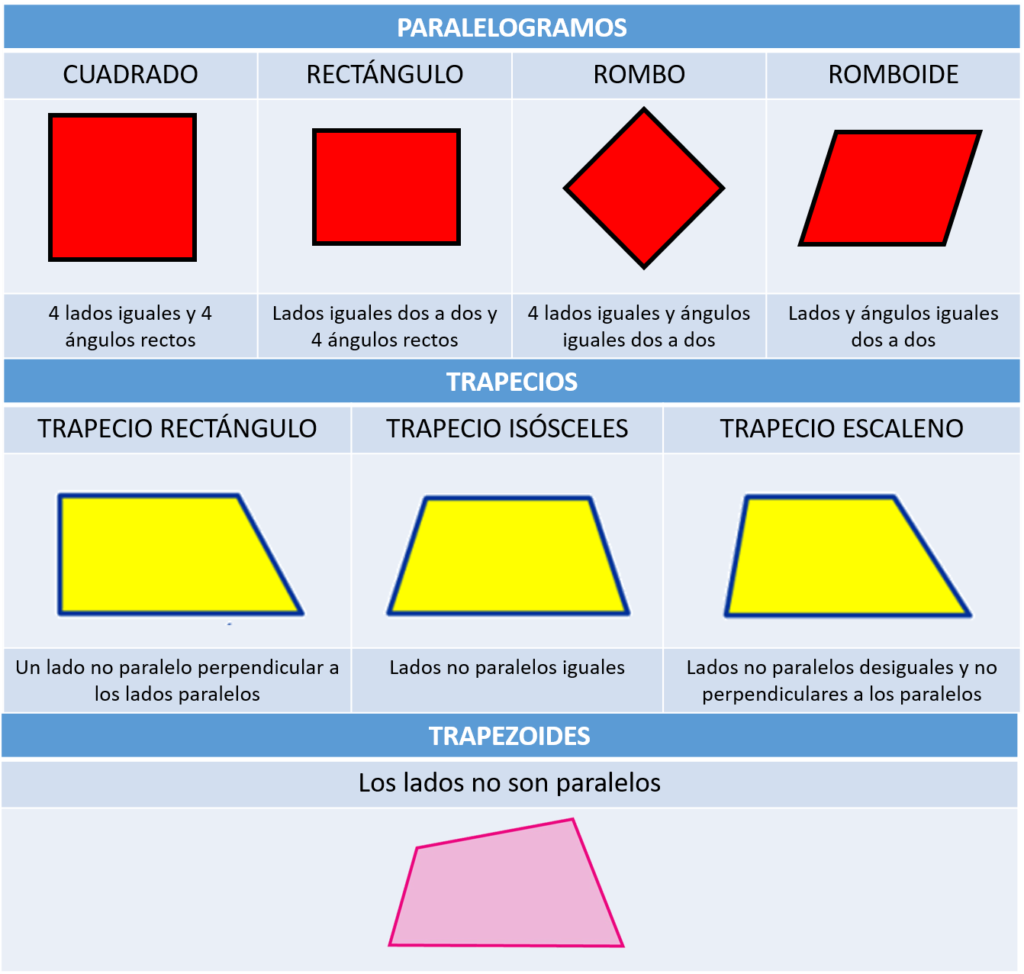
El cuadrilátero es un polígono de cuatro lados y se puede clasificar en:

a) Paralelogramo: Es un cuadrilátero que tiene los lados opuestos paralelos de dos en dos.

b) Trapecio: Es un cuadrilátero que tiene únicamente un par de lados opuestos paralelos.

c) Trapezoide: es un cuadrilátero que no tienen ningún lado paralelo a su opuesto.

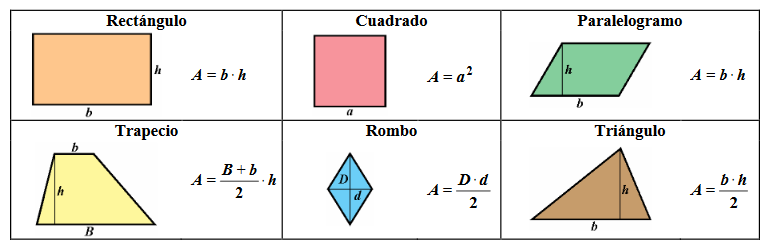
Como en cualquier otra figura geométrica, el perímetro se obtiene sumando la longitud de los 4 lados del cuadrilátero. El área va a depender del tipo de cuadrilátero. A continuación, se muestran los más comunes: 

BIBLIOGRAFÍA

Clemens, S.R., O’Daffer, P. G., Cooney, T. J., & Sullivan, M. (2008). Geometría y trigonometría. Pearson Educación.

Jiménez, R. (2010). Matemáticas II (2da ed.). Pearson Educación.

Guzman, A. (2009). Geometría y trigonometría. Grupo Editorial Patria.

Baldor, J.B. (2004). Geometría plana y del espacio con una introducción a la Trigonometría. Publicaciones Cultural.