7.4. ECUACIONES DE SEGUNDO GRADO O CUADRÁTICAS

La forma general de una ecuación de segundo grado es:

Donde a, b y c con número reales y ‘x’ es la incógnita.

Para resolver ecuaciones de segundo grado existen varios métodos, pero en esta sesión solo estudiaremos dos:

• Fórmula general

• Factorización

8.4.1. ECUACIONES CUADRÁTICAS POR FÓRMULA GENERAL

Las ecuaciones de segundo grado se pueden resolver por medio de la fórmula general, la cual está definido como:

En esta fórmula, a, b y c son los coeficientes señalados en la forma general. Para usar la fórmula general, las ecuaciones de segundo grado deben estar en su forma general, correspondiendo así los valores de a, b y c. Por lo general, las ecuaciones de segundo grado tienen dos soluciones, sin embargo, hay algunas que sólo tienen una solución, además, existen otras que no tienen solución en el campo de los números reales, es decir, su solución es imaginaria.

Paso para resolver una ecuación cuadrática por fórmula general:

PASO 1. En caso de que la ecuación no esté en su forma general, la tenemos que ordenar.

PASO 2. Obtener los valores de a, b y c de la ecuación cuadrática.

PASO 3. Sustituir los valores de a, b y c en la fórmula general.

PASO 4. Resolver la fórmula general para obtener los valores de raíces o soluciones de la ecuación.

EJEMPLO 1. Resolver por medio de la fórmula general la siguiente ecuación

PASO 1. En caso de que la ecuación no esté en su forma general, la tenemos que ordenar.

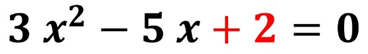
PASO 2. Obtener los valores de a, b y c de la ecuación cuadrática.

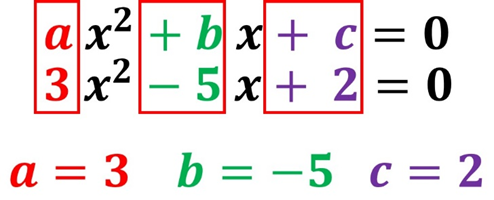
Un error común es que al identificar los coeficientes incluyen indebidamente la x y al sustituir en la fórmula ya no saben qué hacer, ya que la sustitución está mal hecha, es decir, suponen que a=3x² y b = -5x, lo cual, reiteramos, es incorrecto. Otro error entre los estudiantes es que al sustituir los coeficientes se olvidan del signo cuando éstos son negativos. Entonces debemos de tener mucho cuidado con estos dos puntos

PASO 3. Sustituir los valores de a, b y c en la fórmula general.

PASO 4. Resolver la fórmula general para obtener los valores de raíces o soluciones de la ecuación.

Para obtener los valores de las dos raíces o soluciones, una se obtiene al usar el signo positivo y la otra al usar el negativo.

EJEMPLO 2. Resolver por medio de la fórmula general la siguiente ecuación

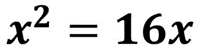
PASO 1. En caso de que la ecuación no esté en su forma general, la tenemos que ordenar.

PASO 2. Obtener los valores de a, b y c de la ecuación cuadrática.

A diferencia del ejemplo anterior, en esta ecuación no existe el valor de c (término independiente) por lo cual se le asigna el valor de cero.

PASO 3. Sustituir los valores de a, b y c en la fórmula general.

PASO 4. Resolver la fórmula general para obtener los valores de raíces o soluciones de la ecuación.

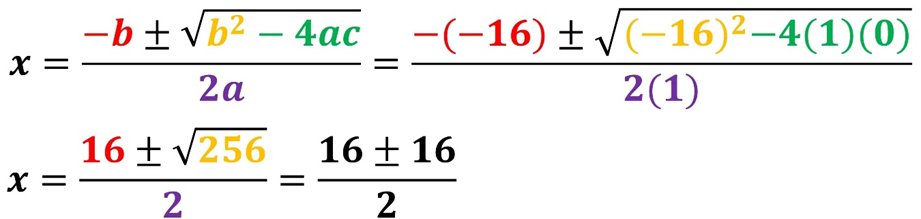
Para obtener los valores de las dos raíces o soluciones, una se obtiene al usar el signo positivo y la otra al usar el negativo.

8.4.2. ECUACIONES CUADRÁTICAS POR FACTORIZACIÓN

Este método para resolver ecuaciones cuadráticas es más sencillo cuando los trinomios son factorizables mediante el método que se estudió en sesiones anteriores.

EJEMPLO 2. Resolver el ejemplo anterior pero ahora por medio de factorización

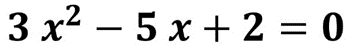
SOLUCIÓN:

PASO 1. Factorizamos el trinomio

PASO 2. Igualamos cada uno de los factores a cero y resolvemos cada uno como si fuera una ecuación normal.

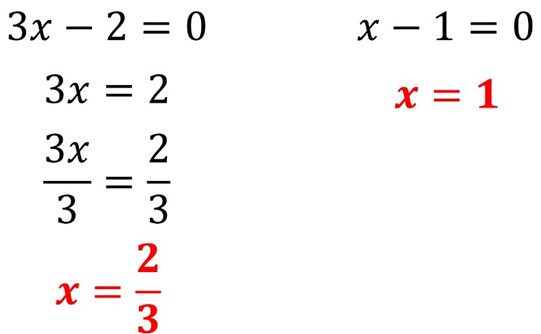
Como podemos observar, obtuvimos los mismos valores que obtuvimos mediante la fórmula general.