10.1. RAZONES TRIGONOMÉTRICAS.
Las razones trigonométricas son las razones existentes entre los lados de un triángulo rectángulo. Se pueden obtener 6 razones con las longitudes de los lados del triángulo rectángulo. Los lados en el triángulo rectángulo se identifican con las letras a, b y c. El lado opuesto al ángulo recto se le llama hipotenusa (c) mientras que a los otros dos lados (a y b) son los catetos del triángulo.

Las funciones trigonométricas de un ángulo agudo en un triángulo rectángulo están definidas por:

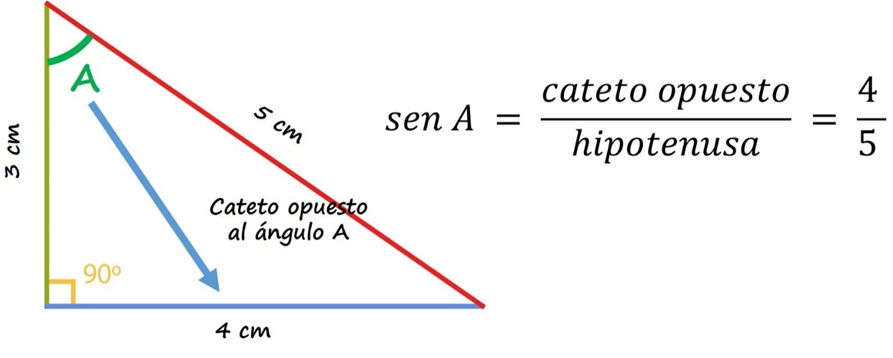
Cada función trigonométrica depende del ángulo agudo que se tome, por ejemplo, en la siguiente figura podemos observar el ángulo A. Si queremos sacar la función seno del ángulo A, tenemos que identificar el cateto opuesto y la hipotenusa. La hipotenusa siempre será el lado opuesto al ángulo recto. El cateto opuesto va a ser el lado opuesto al ángulo que se toma, en este caso el ángulo A. De la figura podemos observar que el valor de la hipotenusa es 5cm mientras que el valor del cateto opuesto es 4cm. Reemplazamos estos valores en nuestra y obtenemos que el Sen(A)=4/5.
EJEMPLO 1: Encontrar los valores de las 6 funciones trigonométricas para el siguiente triángulo:
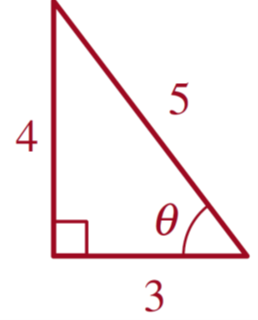
SOLUCIÓN: El primer paso consiste en identificar el ángulo que se utilizará para poder definir el cateto opuesto (co) y el adyacente (ca).

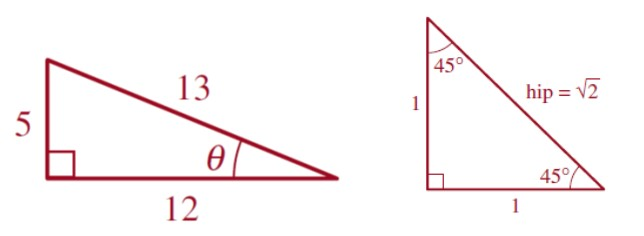
ACTIVIDAD 1: Obtener las 6 funciones trigonométricas para los siguientes triángulos.
11.1.1. IDENTIDADES POR COCIENTE Y RECÍPROCAS
Existen muchas relaciones importantes entre las funciones trigonométricas. Las básicas se presentan a continuación y se denominan identidades fundamentales, y es importante memorizarlas.

EJEMPLO 2: Suponiendo que sen A = 2/3 y cos A = 3/5, encontrar los valores de las razones restantes.
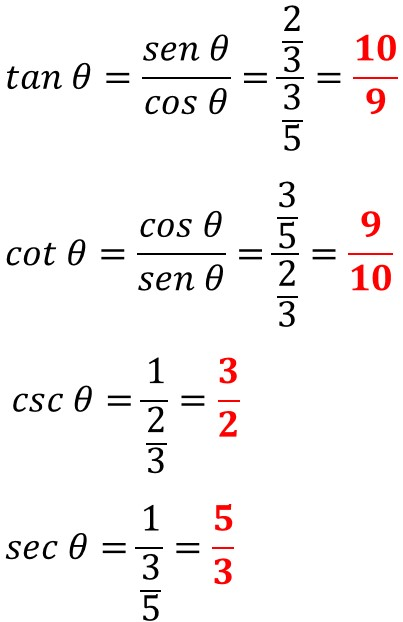
También es importante conocer algunos valores de ciertos ángulos que se utilizarán muy a menudo.
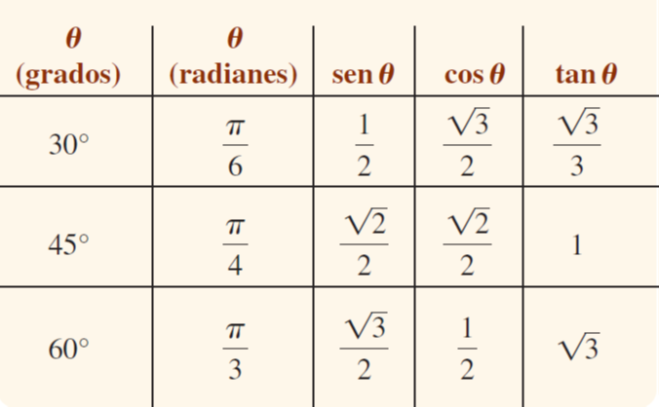
FIGURA 1: Ángulos notables
11.1.2. FUNCIONES TRIGONOMÉTRICAS PARA ANGULO MAYORES A 90°
Los valores de las funciones trigonométricas solamente existen para ángulos comprendidos entre 0 y 90 grados, por eso las tablas trigonométricas solamente traen valores en ese intervalo. Sin embargo, eso no significa que no se puedan obtener, por ejemplo, el seno de 120 grados, o el coseno de 210, o la tangente de 330. Lo que sucede es que el valor de una función trigonométrica mayor de 90 grados corresponde a un valor entre 0 y 90, ya que los grado se repiten cada vez en cada cuadrante del sistema coordenado. Hay que tomar en cuenta que todos los ángulos se miden a partir del eje X positivo, avanzando en el sentido de los cuadrantes, es decir, en sentido contrario a las manecillas del reloj.

FIGURA 2: Ejemplos de ángulos mayores a 90°
Una forma sencilla es encontrar el ángulo de referencia entre 0 y 90° tomando siempre en cuenta el cuadrante en el que se encuentra dicho ángulo. De esta manera se puede obtener el signo de que cada una de las funciones en cada cuadrante.
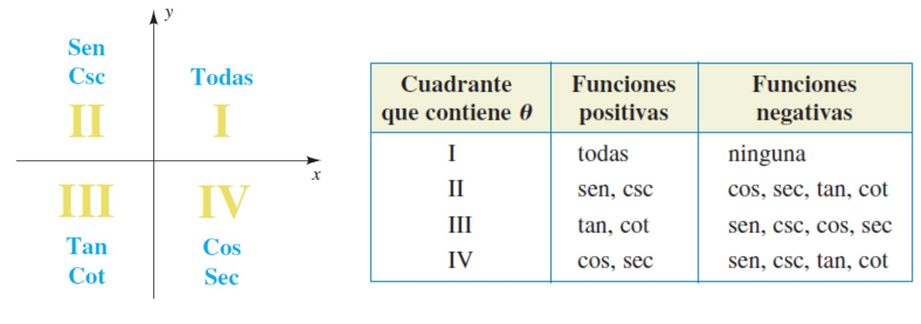
FIGURA 3: Signos de las funciones trigonométricas dependiendo el cuadrante
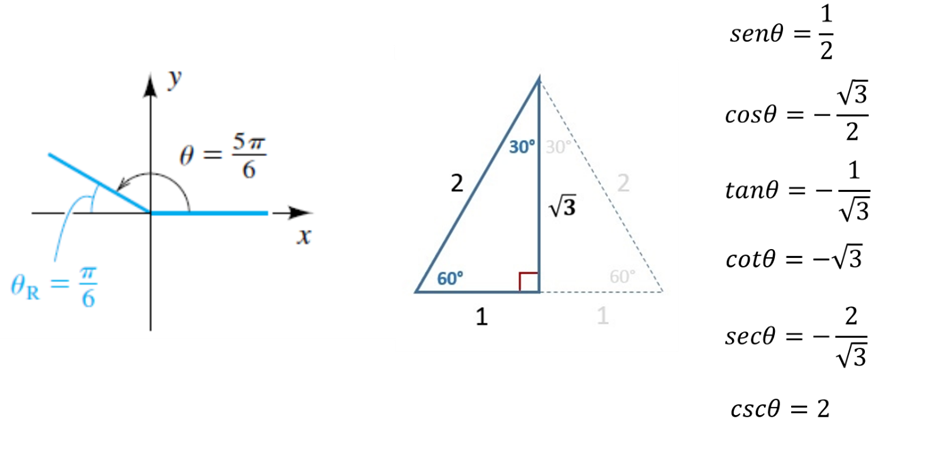
EJEMPLO 3: Encuentre el ángulo de referencia y las funciones trigonométricas para el ángulo siguiente:

SOLUCIÓN: Como vemos en la imagen, el ángulo medido es mayor que 90°, sin embargo, podemos tomar un ángulo de referencia medido desde el eje ‘x’ negativo, para que el ángulo sea menor a 90° y podamos calcular cada una de las funciones trigonométricas. De esta manera el ángulo medido desde ‘x’ negativo será pi/6 (30°) por lo cual calcularemos las funciones trigonométricas de este ángulo y colocaremos el signo correspondiente a cada función en base a la figura 3.
Revisar el siguiente video para el uso correcto de la calculadora para trigonometría
