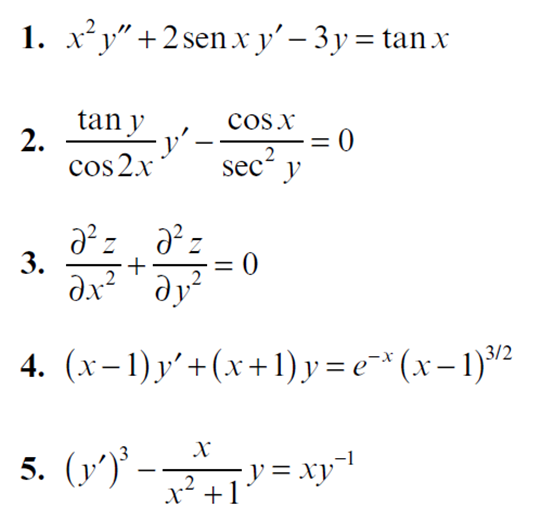1.2. CLASIFICACIÓN DE LAS ECUACIONES DIFERENCIALES

En el curso anterior de algebra aprendimos que para resolver una ecuación del tipo 3x-5=10 hay que realizar un “despeje” de la variable x porque se trata de una ecuación lineal de una variable. Si la ecuación por resolver es de la forma 2x²+3x-9 = 0, sabemos que por tratarse de una ecuación cuadrática (segundo orden), la fórmula general es una opción. Esto nos indica que la clasificación de una ecuación es muy importante ya que nos permite elegir un método de solución adecuado. Con las ecuaciones diferenciales sucede lo mismo. Dada una ecuación diferencial, es importante identificar su tipo y forma para que a partir de esto se elija correctamente el procedimiento de solución. Básicamente, las ecuaciones diferenciales pueden clasificarse de acuerdo con su tipo, orden, linealidad y grado.

Antes de entrar a la clasificación de las ecuaciones diferenciales, es importante saber cómo identificar la variable dependiente y la variable independiente. Debemos de recordar las dos notaciones más utilizadas para representar una derivada: notación prima y la notación de Leibniz

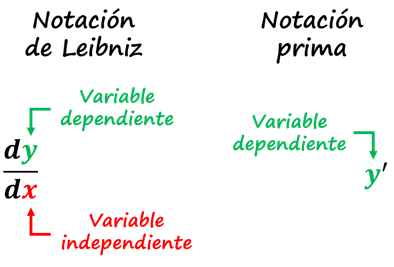
La notación de Leibniz tiene la ventaja sobre la notación prima ya que muestra claramente ambas variables: las dependientes y las independientes

1.2.1 CLASIFICACIÓN DE LAS ECUACIONES DIFERENCIALES DE ACUERDO CON SU TIPO

En esta clasificación podemos encontrar dos grandes grupos: ecuaciones diferenciales ordinarias (EDO) y ecuaciones diferenciales parciales (EDP).

Ecuación diferencial ordinaria. Son aquellas que contienen derivadas de una o más variables dependientes con respecto a una sola variable independiente.

Ecuación diferencial parcial. Son aquellas que contienen contiene la derivada o las derivadas de una o más variables dependientes respecto de dos o más variables independientes.

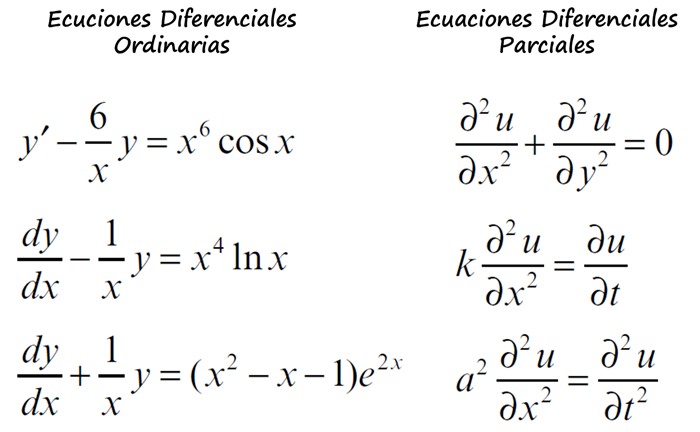
1.2.2. CLASIFICACIÓN DE LAS ECUACIONES DIFERENCIALES DE ACUERDO CON EL ORDEN

El orden de una ecuación diferencial se determina por medio de la mayor derivada de la ecuación.

Debemos tomar en cuenta que el orden de una ecuación diferencial lo determina la derivada más alta, sin importar a que potencia este elevada. Por ejemplo, en la ecuación anterior podemos observar que la derivada más alta es la segunda derivada, y aunque está elevada a la tercera potencia, sigue siendo una ecuación diferencial de segundo orden.

1.2.3. CLASIFICACIÓN DE LAS ECUACIONES DIFERENCIALES DE ACUERDO AL GRADO

Para determinar el orden de una ecuación diferencial consideramos la derivada más alta de la ecuación, sin importar el exponente al que estén elevadas las derivadas y la variable dependiente. Tal exponente se conoce como el grado de la ecuación diferencial. En el siguiente ejemplo podemos observar que la derivada más alta es de segundo orden, sin embargo, esta derivada esta elevada a un exponente 3, por lo cual el grado de la ecuación es 2.

Grado de una ecuación diferencial. La potencia más grande a la cual está elevada una variable dependiente, o bien alguna de sus derivadas, se conoce como grado de una ecuación diferencial.

Recuerda que el grado de la ecuación solo depende de los exponentes de la variable dependiente.

1.2.4 CLASIFICACIÓN DE LAS ECUACIONES DIFERENCIALES DE ACUERDO CON LA LINEALIDAD

Para que una ecuación diferencial sea lineal debe de cumplir 2 condiciones.

CONDICIÓN I. La variable dependiente y todas sus derivadas deben ser de primer grado.

En el anterior ejemplo podemos observar que tenemos derivadas de tercer, segundo, y primer orden, sin embargo, ninguna esta elevada a ninguna potencia.

CONDICIÓN II. Los coeficientes de la variable dependiente y sus derivadas dependen de la variable independiente.

Cualquier ecuación diferencial que cumpla estas dos condiciones será lineal, si no las cumple se denominará como ecuación diferencial no lineal.

ACTIVIDAD: Clasificar las siguientes ecuaciones diferenciales de acuerdo a las 4 clasificaciones descritas en esta sesión. Recuerda subir tu actividad a classroom