3.1.FUNCIONES HOMOGÉNEAS

En algebra se aprende que, si una función polinomial tiene todos sus términos del mismo grado, entonces la función se denomina homogénea. Este concepto puede extenderse a cualquier tipo de función en dos variables, y nos permitirá resolver una ecuación diferencial que puede no ser separable. Por esta razón es muy importante saber identificar una función homogénea. La manera más sencilla es mediante la suma de los exponentes de cada término de la función polinomial. Por ejemplo, supongamos que queremos definir si la siguiente función es homogénea:

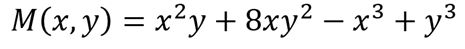
Para determinar si la función es homogénea, debemos sumar los exponentes de ambas variables de cada término. Podemos ver que el en el primer término la ‘x’ tienen un exponente 2 y la ‘y’ un exponente 1 por lo que la suma de los exponentes del primer término es x²y → 2 + 1 = 3; la suma de los exponentes del segundo término es 8x²y → 1 + 2 = 3; la suma del tercer término es x³ → 3, y la suma del cuarto término es y³ → 3. Ya que la suma de los exponentes de los 4 términos es la misma podemos deducir que la función es homogénea y de grado 3.

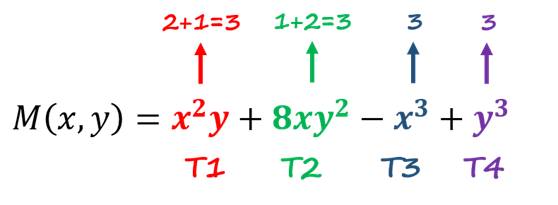
Sin embargo, este método no es útil para todas las funciones, por lo cual, otra forma de encontrar el grado de homogeneidad de una función es sustituir ‘x’ por kx, y ‘y’ por ky. Este método se explica en el siguiente video.