1.1. MÉTODOS PARA LA DETERMINACIÓN DE RAÍCES
Un método para obtener una solución aproximada consiste en graficar la función y determinar dónde cruza el eje de las x. Este punto, que representa el valor de x para el cual f (x) = 0, es la raíz. Aunque los métodos gráficos son útiles en la obtención de estimaciones de las raíces, tienen el inconveniente de que son poco precisos. Un método alternativo es el de prueba y error. Esta “técnica” consiste en elegir un valor de x y evaluar si f (x) es cero. Si no es así (como sucederá en la mayoría de los casos) se hace otra elección y se evalúa nuevamente f (x) para determinar si el nuevo valor frece una mejor aproximación de la raíz. El proceso se repite hasta que se obtenga un valor que proporcione una f (x) cercana a cero. Las técnicas descritas a continuación representan alternativas que no sólo aproximan, sino que emplean estrategias sistemáticas para dirigirse a la raíz verdadera.
Para la determinación de raíces reales de ecuaciones algebraicas y trascendentes se utilizan técnicas se diseñaron para determinar el valor de una sola raíz real basándose en un conocimiento previo de su posición aproximada. Se conocen los métodos cerrados, que usan intervalos, para encontrar raíces. Estos métodos empiezan con intervalos que encierran o contienen a la raíz, y después reducen sistemáticamente el tamaño del intervalo. Dentro de estos se encuentra el de bisección. Por su parte, los métodos abiertos son métodos también emplean iteraciones sistemáticas de prueba y error; pero no requieren que el intervalo inicial encierre a la raíz. Se descubrirá que estos métodos, en general, son más eficientes que los métodos cerrados, aunque no siempre funcionan. Dentro de ellos se encuentra el de Newton-Raphson.
Método de bisección
En general, si f(x) es real y continúa en el intervalo que va desde xl hasta xu y f (xl) y f (xu) tienen signos opuestos, es decir,

El método de bisección, conocido también como de corte binario, de partición de intervalos o de Bolzano, es un tipo de búsqueda incremental en el que el intervalo se divide siempre a la mitad. Si la función cambia de signo sobre un intervalo, se evalúa el valor de la función en el punto medio. La posición de la raíz se determina situándola en el punto medio del subintervalo, dentro del cual ocurre un cambio de signo. El proceso se repite hasta obtener una mejor aproximación.
Algoritmo

Ejemplo
Determinar el coeficiente de resistencia c necesario para que un paracaidista de masa m = 68.1 kg tenga una velocidad de 40 m/s después de una caída libre de t = 10 s. Nota: La aceleración de la gravedad es de 9.81 m/s2.
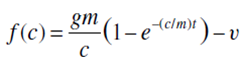
Solución El primer paso del método de bisección consiste en asignar dos valores iniciales a la incógnita (en este problema, c) que den valores de f(c) con diferentes signos. Basándonos en la siguiente figura, podemos identificar entre que valores se encuentra
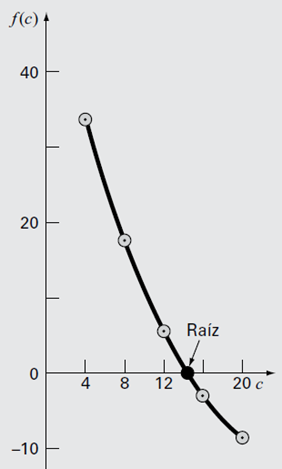
Se observa que la función cambia de signo entre los valores 12 y 16. Por lo tanto, la estimación inicial de la raíz xr se encontrará en el punto medio del intervalo
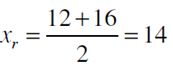


Método de Newton-Raphson
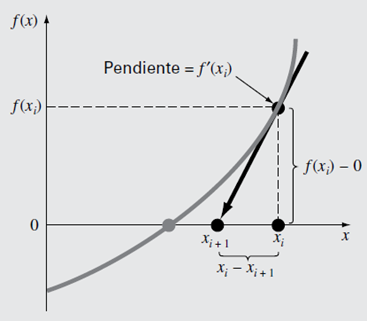
Tal vez, la fórmula de Newton-Raphson sea la más ampliamente utilizada. Si el valor inicial para la raíz es xi, entonces se puede trazar una tangente desde el punto [xi, f(xi)]. Por lo común, el punto donde esta tangente cruza al eje x representa una aproximación mejorada de la raíz.
Se tiene que la primera derivada en x es equivalente a la pendiente:
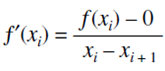
Çque se arregla para obtener
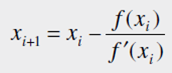
la cual se conoce como fórmula de Newton-Raphson.
Ejemplo

que se sustituye, junto con la función original en
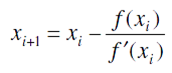
para tener

