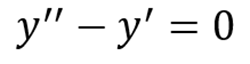1.3. CLASIFICACIÓN DE LAS SOLUCIONES DE UNA ECUACIÓN DIFERENCIAL

Las soluciones de una ecuación diferencial, al igual que las propias ecuaciones, también tienen una clasificación. Básicamente, las soluciones se clasifican en implícitas y explícitas, solución general, soluciones particulares y soluciones singulares. Antes de entrar en esta clasificación es importante recordar que la solución de una ecuación diferencial es una función. Veámoslo con un ejemplo:

EJEMPLO 1: Verificar si la función a) y=e^x  y b) y=e^2x  son soluciones de la siguiente ecuación diferencial:

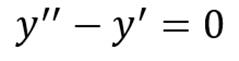
SOLUCIÓN: Como lo mencionamos anteriormente, la solución de una ecuación diferencial es una función. Para comprobar si esta función es una solución de la ecuación, tenemos que realizar el mismo procedimiento que utilizábamos en una ecuación algebraica. Vamos a sustituir la función y sus derivadas en la ecuación, por lo que el primer paso es encontrar las derivadas de las funciones:

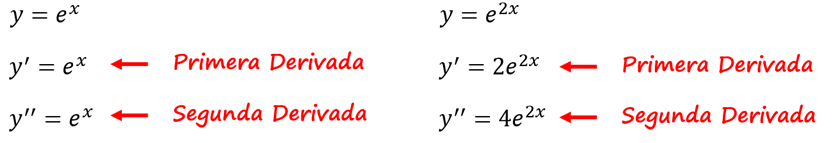
Una vez que encontramos las derivadas, sustituimos en la ecuación diferencial y comprobamos si se cumple o no la igualdad

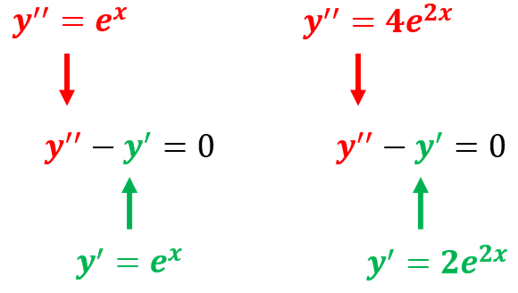
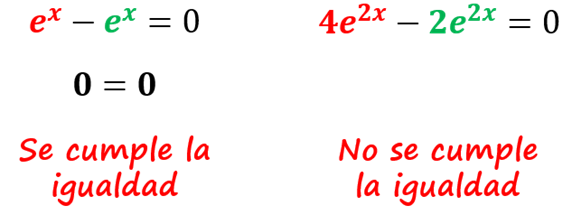
Como podemos observar en el primer caso si se cumple la igualdad por lo que y=e^x si es una solución de la ecuación. Sin embargo, en el segundo caso no se cumple la igualdad por lo que y=e^2x no es una solución.

1.3.1. SOLUCIONES IMPLICITAS Y EXPLICITAS

En términos simples, una solución está dada en forma explícita si aparece “despejada” alguna de las variables en términos de la otra, y en caso contrario, cuando no aparece completamente despejada ninguna de las variables, la solución está dada en forma implícita. Las solución del ejemplo anterior estaban dadas en forma explícita, ya que la variable ‘y’ estaba despejada en términos de ‘x’.

1.3.2. SOLUCIÓN GENERAL, SOLUCIONES PARTICULARES Y LA SOLUCIÓN TRIVIAL

Otra manera de clasificar las soluciones de una ecuación diferencial se basa en si contienen o no constantes arbitrarias. Las constantes arbitrarias aparecen en una solución como resultado de agregar constantes de integración en el proceso de solución. Para el caso de una ecuación diferencial ordinaria, el número de constantes arbitrarias coincide con el orden de la ecuación.

Si una solución contiene n parámetros arbitrarios, entonces se dice que la función es una familia de soluciones o solución general.

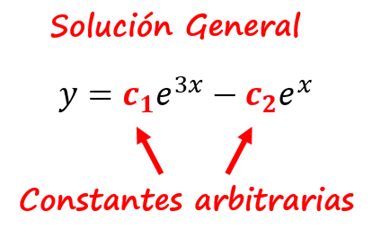
Si una solución no contiene parámetros arbitrarios, se dice que es una solución particular

Por último, si la función y=0 es una solución entonces decimos que y=0 es la solución trivial.

ACTIVIDAD 2: Verificar si la función y=e^-x es una solución siguiente ecuación diferencial: