1.3. OPERACIONES BÁSICAS CON FRACCIONES
La división exacta entre dos números no siempre es posible. Por ejemplo, la división entre 4 y 5 no es exacta, ya que no existe ningún número entero que multiplicado por 5 nos de 4. Entonces, ¿cómo podemos expresar el resultado de esta operación? Muy fácil, por medio del número fraccionario 4/5. Una fracción representa un valor numérico derivado del cociente de dos números, es decir, es una división sin realizar.
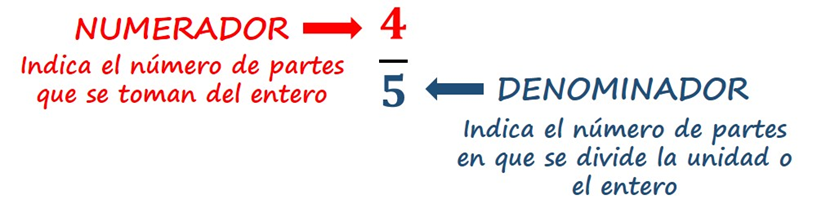
Una fracción está compuesta por dos elementos: numerador y denominador. El denominador indica en cuantas partes iguales se ha dividido la unidad principal, y el numerador, cuantas partes se toman.
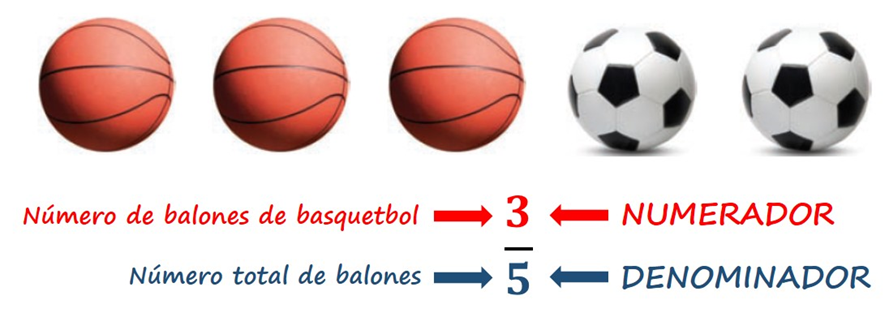
También, una fracción puede representar una parte de un conjunto de cosas. Por ejemplo, en la siguiente figura hay 5 balones de los cuales 3 son de basquetbol, por lo cual se puede decir que 3/5 (tres quintos) de los balones son de basquetbol.
1.3.1 FRACCIONES EQUIVALENTES
Las fracciones equivalentes son fracciones que representan la misma cantidad, aunque el numerador y el denominador sean diferentes, por ejemplo, si partimos la unidad en 2 partes iguales y tomamos una, es lo mismo que si partimos la unidad en 4 partes iguales y tomamos 2 partes.
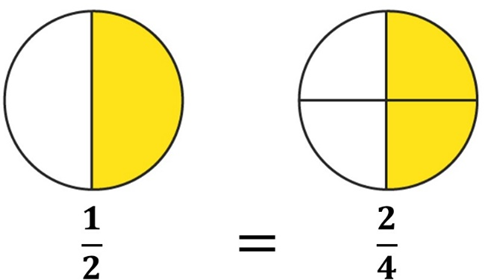
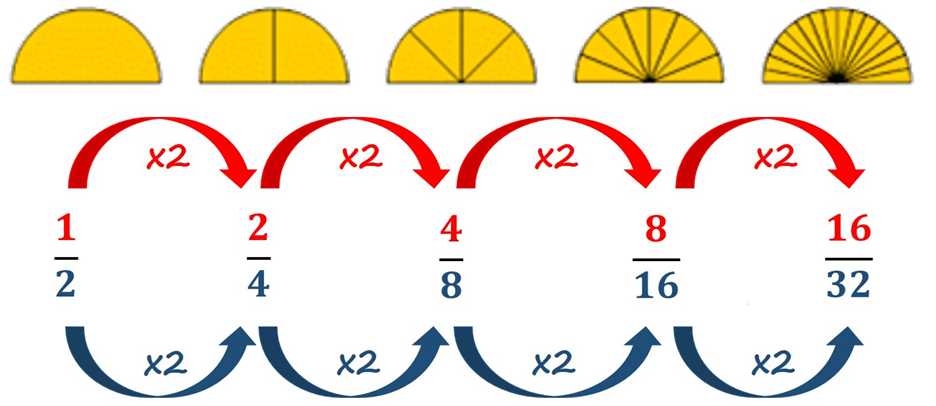
IMPORTANTE: Recuerda que tú puedes crear fracciones equivalentes multiplicando o dividiendo el denominador por el mismo número:
Supongamos que queremos convertir 7/8 (siete octavos) a una fracción equivalente que tenga como denominador 24:

Para realizar la conversión, la primera pregunta que tenemos que hacernos es, ¿Qué número multiplicado por 8 nos da como resultado 24?
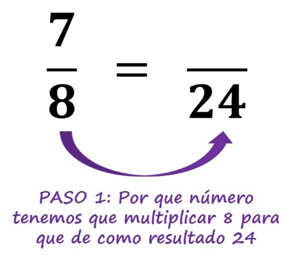
La respuesta sería 3, ya que 3×8=24, entonces el número de arriba también lo tendríamos que multiplicar por 3 para obtener su fracción equivalente.
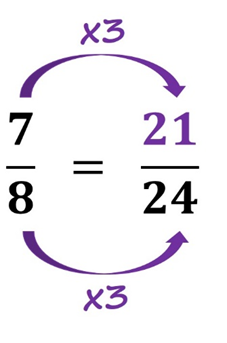
Por lo cual, nuestro resultado sería 21/24. Este procedimiento es muy utilizado principalmente para poder realizar sumas y restas de fracciones con diferente denominador, por lo cual, lo utilizaremos en un tema posterior en esta sesión.
1.3.2. SIMPLIFICACIÓN DE FRACCIONES
Como vimos en la sección anterior, todas las fracciones equivalentes entre sí representan el mismo valor. Por lo cual, nos interesa emplear la fracción más simple, es decir, la que tenga el numerador y denominador más pequeño. Para simplificar una fracción, nos valemos del concepto de fracción equivalente ya que sabemos que si dividimos al numerador y al denominador por el mismo número, obtenemos otra fracción equivalente.
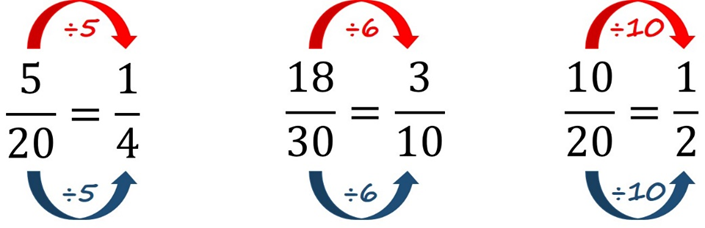
Para simplificar una fracción debemos buscar un número que pueda dividir al numerador y denominador. Intentaremos siempre encontrar el número más grande que divida ambos, ese número es el máximo común divisor (MCD) de ambos, así, de una sola vez, habremos llegado al resultado.
En el primer ejemplo de la imagen tenemos que encontrar el número más grande que pueda dividir al 5 (numerador) y al 20 (denominador), que en este caso es el número 5.
ACTIVIDAD 1: Simplifica las siguientes fracciones a su mínima expresión. Recuerda subir tu actividad a classroom.
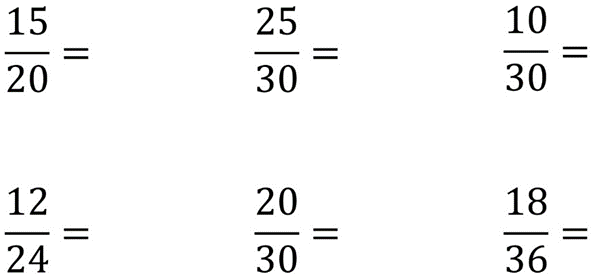
1.3.3. SUMA Y RESTA DE FRACCIONES
Para sumar o restar fracciones, es necesario que todas tengan el mismo denominador. En este caso se suman o restan los numeradores y se mantiene el mismo denominador.
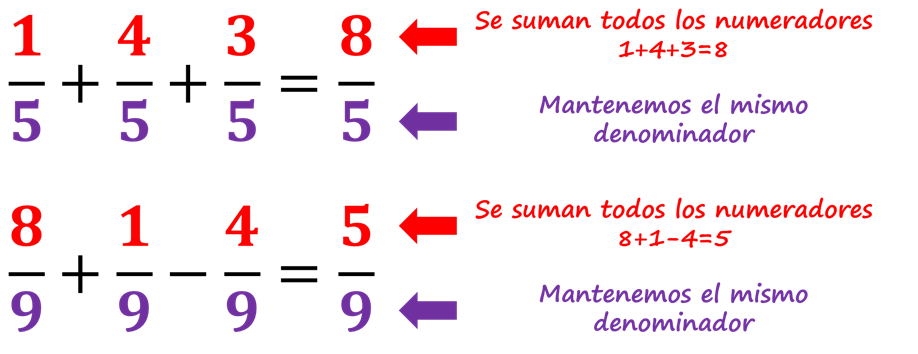
IMPORTANTE: Recuerda que para poder realizar una suma o resta de fracciones los denominadores de las fracciones deben de ser iguales.
En caso de que las fracciones tengan un denominador diferente, tenemos que reescribir las fracciones como fracciones equivalentes con el mismo denominador.
EJEMPLO 1: Realizar la siguiente operación con fracciones

SOLUCIÓN: Como el denominador de las fracciones es diferente, las operaciones no se pueden realizar directamente, por lo cual, el primer paso consiste en encontrar el mínimo común múltiplo (MCM) entre los denominadores. Para conocer un método de cómo obtener el MCM entre 3 números, revisa el siguiente video:
El MCM entre los 3 denominadores es 24, por lo cual, tenemos que convertir cada una de las fracciones, a su fracción equivalente con un denominador 24, como lo vimos en un tema posterior.

Una vez que tengan el mismo denominador, realizamos las operaciones en el numerador para obtener el resultado final.

2.4.2. MULTIPLICACIÓN DE FRACCIONES
Para multiplicar fracciones no es necesario que tengan el mismo denominador, simplemente se multiplica directamente: multiplicamos los numeradores y los denominadores.

2.4.3. DIVISIÓN DE FRACCIONES
Para dividir dos fracciones, se tiene que multiplicar de manera cruzada, como se muestra en el siguiente ejemplo:

ACTIVIDAD 2: Realiza las siguientes operaciones. Recuerda subir tu actividad a classroom.

