2.1. ANTIDERIVADA (INTEGRAL INDEFINIDA)

Por su mismo nombre, antiderivada, podemos deducir que es la operación contraria a la derivada, pero, ¿Qué diferencia tiene con el concepto de integral definida que vimos en la sesión anterior? .

La antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada. Veamos el siguiente ejemplo.

EJEMPLO 1: Encontrar la antiderivada de la siguiente función

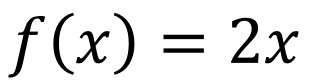
SOLUCIÓN: Para encontrar la solución, tenemos que pensar en una función que al derivarla nos dé como resultado 2x. Recordando nuestro curso de cálculo diferencial, podríamos decir en primera instancia que la antiderivada de esta función es x² ya que la derivada de x² es 2x, sin embargo, no es la única antiderivada.

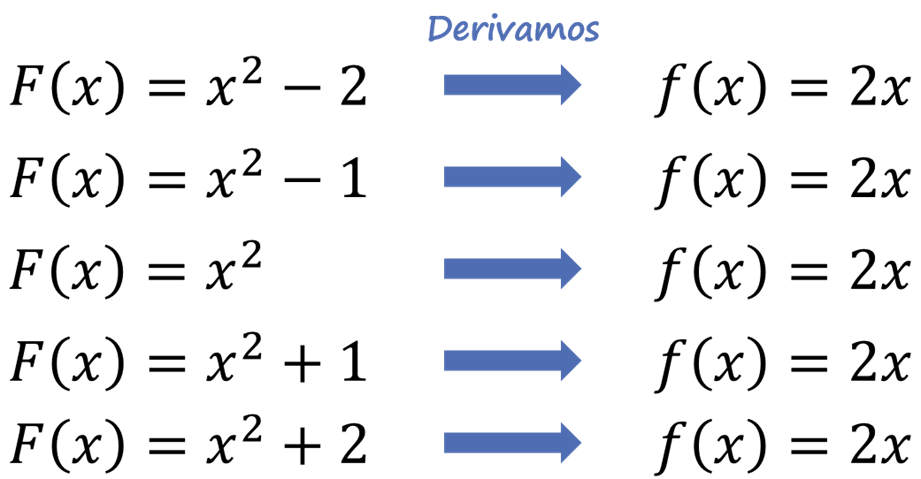
En la imagen anterior podemos observar que F(x)= x² no es la única respuesta a nuestra pregunta ya que diferentes funciones, al derivarlas, dan el mismo resultado. Con esto podemos llegar a la conclusión de que si una función f tiene una antiderivada, entonces tendrá una familia de ellas, y la diferencia entre cada una de estas será la constante.  Pero, ¿Cómo representamos esta familia de funciones? Debemos de tener claro que no podemos escribir todas las funciones de la familia ya que son infinitas (x²+1, x²+2, x²+3, …), por lo cual, utilizaremos la letra C para representar esa constante F(x)= x²+C. Como x²+C describe todas las antiderivada de 2x, podemos referirnos a esta como la antiderivada general de 2x denotada por

Que se lee como la integral indefinida de 2x con respecto a x.

Como nos damos cuenta, utilizamos el signo de la integral para representar la antiderivada pero, ¿Qué diferencia hay entre el concepto que vimos en la sesión anterior? La respuesta a esta pregunta está en la palabra “indefinida” y la diferencia está en que este tipo de integral no tiene definido el intervalo o límites de integración.