2. ÁNGULOS

En geometría, un ángulo se puede definir como la abertura comprendida entre dos segmentos rectilíneos con un punto extremo en común. Los segmentos son los lados del ángulo, mientras que el punto donde se unen se le llama vértice. La bisectriz de un ángulo es la semirrecta que tienen como origen el vértice y divide al ángulo en dos ángulos iguales.

En trigonometría con frecuencia interpretamos a los ángulos como rotaciones de una semirrecta. A una de estas semirectas se le llama lado inicial y al otro lado final o terminal. El ángulo formado se identifica señalando la dirección y cantidad de rotación desde el lado inicial hasta el lado final:

• Si la rotación es en sentido contrario de las manecillas del reloj, el ángulo es positivo
• Si la rotación es en sentido de las manecillas del reloj, el ángulo es negativo.

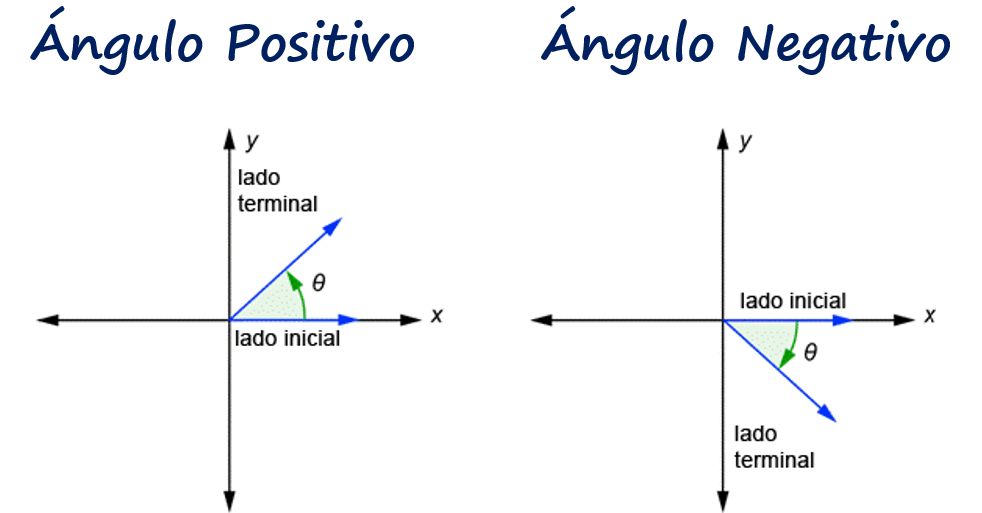
FIGURA 1: Ejemplo de un ángulo positivo y un ángulo negativo.

2.1 MEDIDAS DE UN ÁNGUL

Entre las mediciones más usuales de un ángulo encontramos el grado sexagesimal. Esta medición se basa en que una vuelta completa mide 360°, por lo cual un grado equivale a dividir una vuelta completa en 360 partes.

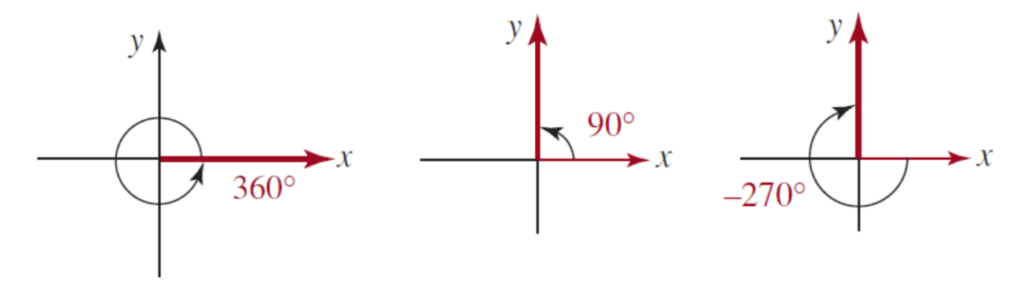
FIGURA 2: Ejemplos de Ángulos en grados

Por lo regular, la fracción de un grado se determina mediante decimales, sin embargo, también se puede expresar mediante minutos y segundos, donde:

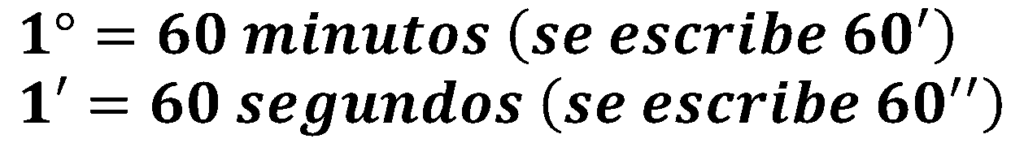
EJEMPLO 1:  Convertir

1. 35.28° a grados, minutos y segundos
2. 10° 46’ 32’’ a grados con decimal

SOLUCIÓN

• Separamos los enteros y los decimales de la cifra en grados. La parte decimal se multiplica por 60 y el resultado serán los minutos.

Del resultado anterior separamos la cifra de los minutos en enteros y decimales. La parte decimal se multiplica por 60, y después se juntas ambos resultados para formar el resultado final.

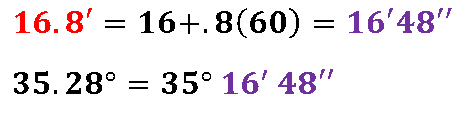
• Separamos la cifra en grados, minutos y segundos.  Lo grados quedan igual, mientras que los minutos se dividen entre 60 y los segundos entre 3600. Para obtener el valor final se suman las 3 cifras.

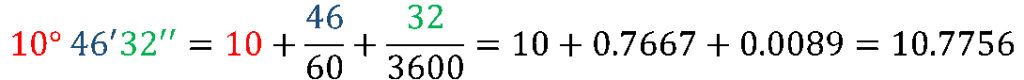
ACTIVIDAD 1: Realizar los siguientes ejercicios como en el ejemplo anterior.
a) Convertir 20.5° a grados, minutos y segundos.
b) 98° 10’ 40’’ a grados con decimal.

En el cálculo, la medida más utilizada para la medición de ángulos, es el radian. Una vuelta completa de 360° representa 2π radianes.

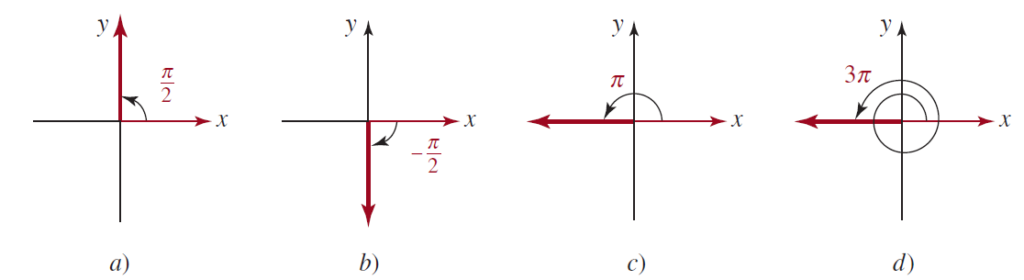
FIGURA 3: Ejemplos de ángulos en radianes.

Si representamos por S la medida de un ángulo en grados sexagesimales y por R la medida de un ángulo, pero en radianes, podemos establecer las siguientes fórmulas de conversión:

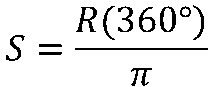
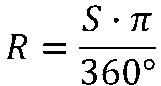
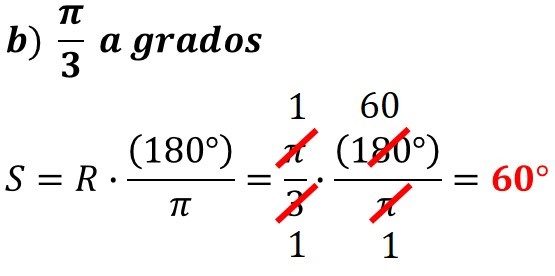
EJEMPLO 2: Convertir las siguientes expresiones.

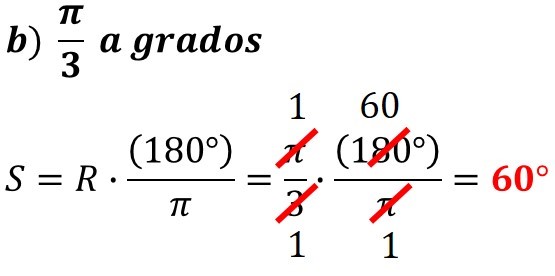
ACTIVIDAD 2: Realizar los siguientes ejercicios como en el ejemplo anterior
a) 60° a radianes
b) π/12 a grados

BIBLIOGRAFÍA

Jiménez, R. (2010). Matemáticas II (2da ed.). Pearson Educación.

Clemens, S.R., O’Daffer, P. G., Cooney, T. J., & Sullivan, M. (2008). Geometría y trigonometría. Pearson Educación.

Guzman, A. (2009). Geometría y trigonometría. Grupo Editorial Patria.

Baldor, J.B. (2004). Geometría plana y del espacio con una introducción a la Trigonometría. Publicaciones Cultural