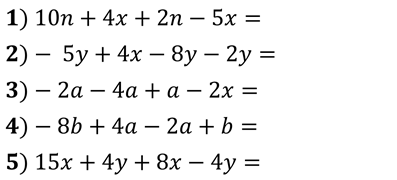5.1: REDUCCIÓN DE TÉRMINOS SEMEJANTES (SUMA Y RESTA)

Cuando dos términos contienen las mismas variables elevadas a los mismos exponentes, se dice que son términos semejantes.

La reducción de términos semejantes consiste en hacer las operaciones involucradas en la expresión algebraica en la que se encuentran, y con ello, convertir en un solo término dos o más términos semejantes. Consideremos el ejemplo de las manzanas y los globos, pero en vez de colocar objetos cotidianos, coloquemos letras que representen a cada objeto.

En el primer ejemplo, colocaremos en vez de la manzana una ‘x’ y en vez de los globos una ‘y’. Esto porque son diferentes objetos, por lo cual, necesitamos utilizar diferentes letras. Como lo comentamos en la primera sección, esta operación no se puede realizar debido que no son términos semejantes. A diferencia de la primera suma, la segunda si se puede realizar, ya que son términos semejantes. Decimos que una expresión algebraica está simplificada cuando no tienen términos semejantes por agruparse.

IMPORTANTE: Las variables en una expresión algebraica representan algún tipo de número, por lo cual deben de seguir las mismas reglas de suma y resta, incluyendo las leyes de los signos.

EJEMPLO 1: Reducir la siguiente expresión algebraica

SOLUCIÓN: Primero tenemos que identificar los términos semejantes en la expresión algebraica y realizar cada una de las operaciones por separado de la siguiente forma:

EJEMPLO 2: Reducir la siguiente expresión algebraica

SOLUCIÓN: Como lo mencionamos anteriormente, las variables en una expresión algebraica representan números, por lo cual, debemos seguir exactamente las mismas reglas que en una expresión aritmética. El primer paso es quitar los paréntesis y realizar las operaciones en caso de que sea posible. Para este ejemplo, solamente se tienen que realizar leyes de los signos, y como ambos signos antes del paréntesis son positivos, los signos de cada término deben permanecer iguales. Así que quitamos los paréntesis manteniendo el mismo signo en cada uno de los términos.

Después identificamos los términos semejantes dentro de la expresión algebraica.

Realizamos la operación de cada uno de los términos semejantes siguiendo las leyes de los signos.

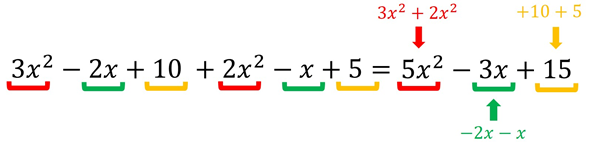
EJEMPLO 3: Reducir la siguiente expresión algebraica

SOLUCIÓN: A diferencia del anterior, aquí ya tenemos un signo menos antes del segundo paréntesis. Este signo va a afectar a todos los términos que se encuentren dentro del segundo paréntesis cambiando su signo, es decir, los positivos cambiarán a negativos y los negativos a positivos. Solo cambiarán de signo los términos que se encuentren dentro del paréntesis que está inmediatamente después del signo menos.

Identificamos los términos semejantes dentro de la expresión algebraica.

Realizamos la operación de cada uno de los términos semejantes siguiendo las leyes de los signos.

ACTIVIDAD 1: Realiza los siguientes ejercicios. Recuerda subir tu actividad a Classroom