5.2. APLICACIÓN DE ECUACIONES DIFERENCIALES EN CIRCUITOS ELÉCTRICOS

Una fuerza electromotriz, generalmente una batería, produce un voltaje de E(t), medida en volts (V) y una corriente I(t) medida en amperes (A) en cualquier instante t. Supongamos un circuito con  un resistor de resistencia de R ohms (Ω) y un inductor con una inductancia de L henrios (H). La ley de Ohm proporciona la caída de voltaje debida al resistor como RI. La caída de voltaje ocasionada por el inductor es L di/dt. Una de las leyes de Kirchhoff establece que la suma de la caída de voltaje es igual al voltaje proporcionado E(t). Por lo que tenemos L di/dt + RI = E(t) lo cual es una ecuación diferencial lineal de primer orden. La solución proporciona la corriente I en el tiempo t.

EJEMPLO 1: Se aplica una fuerza electromotriz de 10V a un circuito LR en serie. El valor de la inductancia es de 0.1 Henrios y el valor de la resistencia es de 50Ω. Determine la corriente i(t), si la corriente i(0)=0.

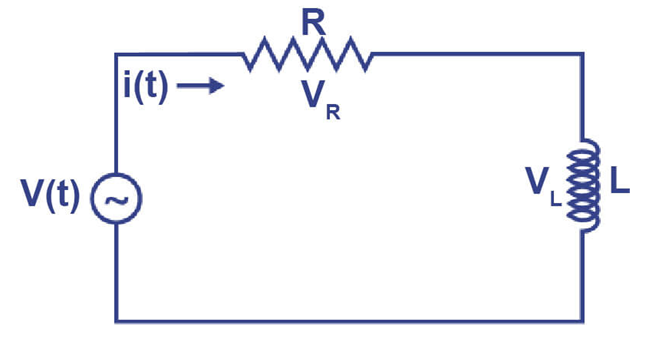
Figura 1: https://electronicaonline.net/electronica/circuito-rl-funcionamiento-usos/:

SOLUCIÓN: Primero tenemos que recordar de nuestro curso de análisis de circuitos, que, a diferencia de una resistencia, la corriente en un inductor cambia con respecto al tiempo. Para obtener el modelo matemático tendremos que recordar las leyes de Kirchoff:

LEY DE CORRIENTE DE KIRCHOFF. La suma de las corrientes hacia (o desde) cualquier punto es cero.

LEY DE VOLTAJES DE KIRCHOFF. Alrededor de cualquier trayectoria cerrada la suma de las caídas de voltaje instantáneas en una dirección específica, es cero.

Para este ejemplo queremos encontrar el valor de la corriente en un circuito cerrado por lo cual utilizaremos la LEY DE VOLTAJES. En la siguiente tabla podemos observar como se representa matemáticamente las caídas de voltajes para cada elemento del circuito.

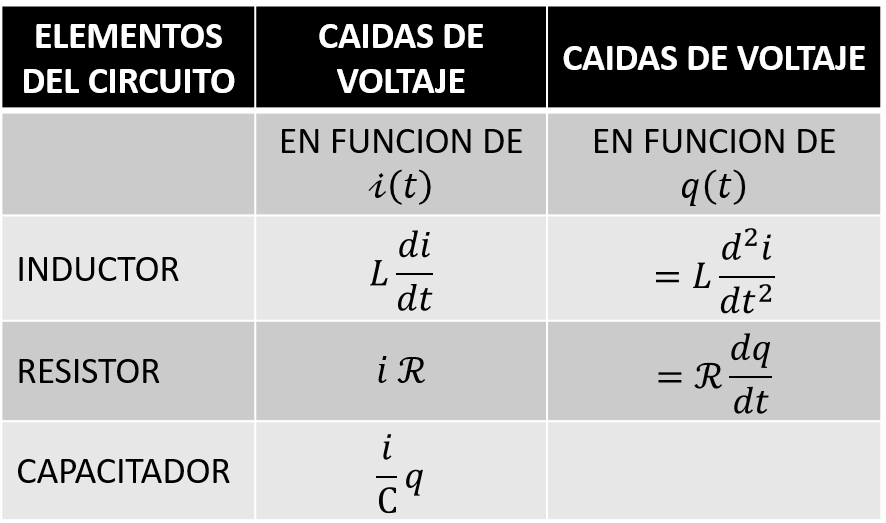
Aplicando la ley de mallas de Kirchoff al circuito obtenemos la siguiente ecuación:

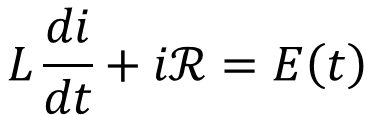
Donde L y R son constantes conocidas como la inductancia y la resistencia, respectivamente. La corriente i(t) representa la solución a esta ecuación. Una vez obtenida la ecuación diferencial el siguiente paso consiste en sustituir los valores de inductancia y resistencia descritos en el problema:

Analizando esta ecuación podemos observar que no pertenece a ninguna de las clasificaciones vistas en sesiones anteriores (homogénea, exacta o de variables separables) por lo cual en la siguiente sección se describirá un método alternativo para resolver este tipo de ecuaciones.