5.2. REGLAS DE LOS EXPONENTES
1° Ley. La multiplicación de dos cantidades de la misma base, es igual a tomar la misma base y sumar los exponentes.

2° Ley. La división de dos cantidades de la misma base, es igual a tomar la misma base y restar los exponentes.
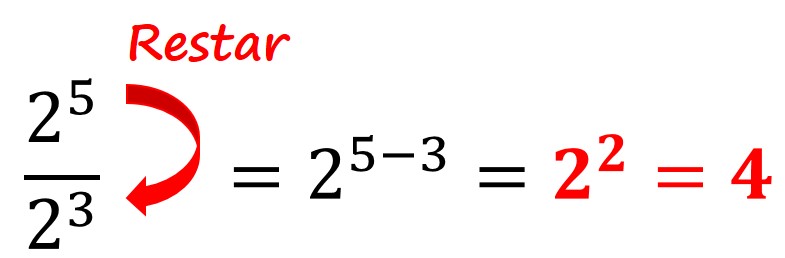
Ahora, ¿Qué pasa si el exponente de arriba es mayor que el exponente de abajo? Tenemos que aplicar el mismo procedimiento, restar el exponente del numerador menos el exponente del denominador, tomando en cuenta que el resultado saldrá negativo.
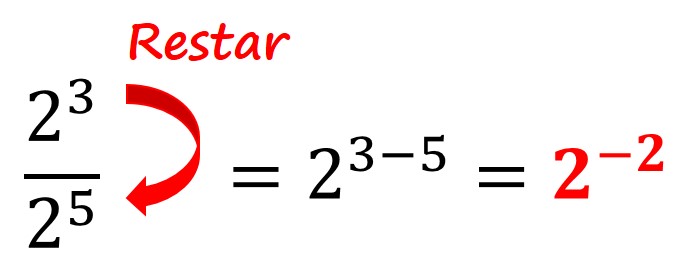
3° Ley. Si la multiplicación de dos o más cantidades cualesquiera está elevada a una potencia, todos los factores toman el mismo exponente.


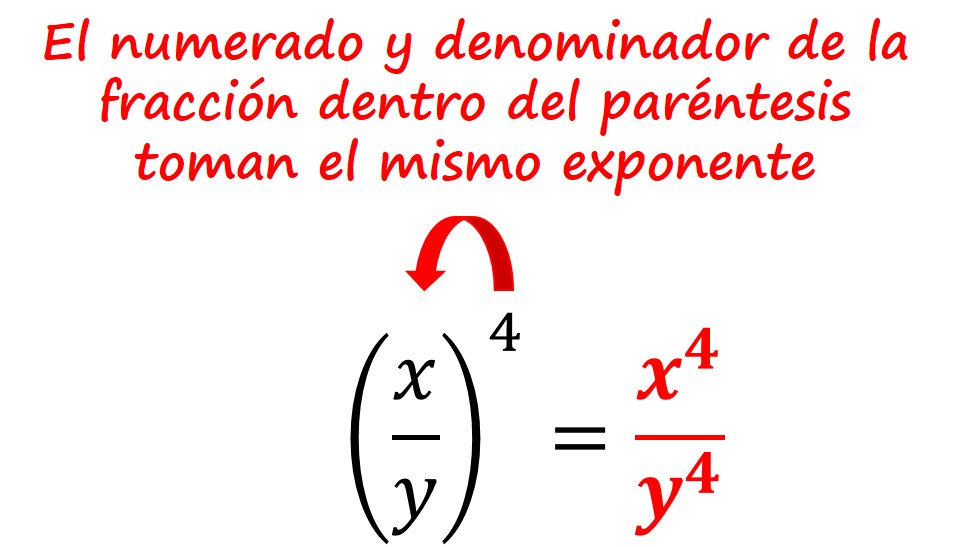
4° Ley. Si la división de dos cantidades cualesquiera está elevada a una potencia, tanto el numerador como el denominador toman el mismo exponente.

5° Ley. Si una expresión exponencial se eleva a una potencia, se toma la misma base y se multiplican los exponentes.

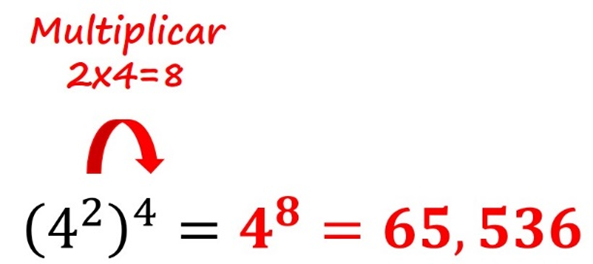
6° Ley. Toda expresión con exponente negativo, es igual a su recíproco.
El recíproco de un número es simplemente 1 entre el número. Es decir, el recíproco de 5 es 1/5 (un quinto). La multiplicación de un número por su recíproco siempre va a ser 1.
Toda expresión con exponente negativo la podemos convertir a exponente positivo para poder resolverla. Veamos el siguiente ejemplo:

Una vez que convertimos el exponente negativo a positivo, podemos resolver cada la operación.

7° Ley. Toda cantidad elevada a la potencia cero, es igual a uno.
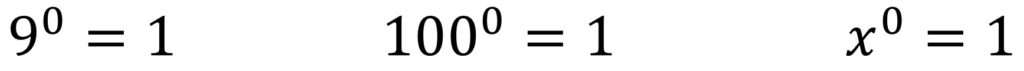
8° Ley. Un número elevado a una potencia fraccionaria es igual a la raíz de ese número.
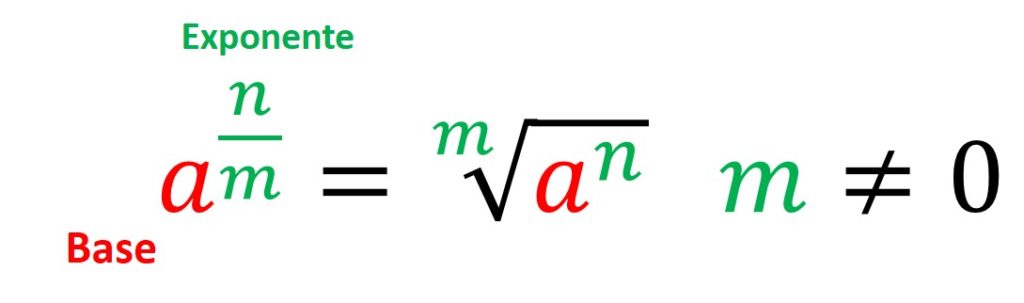
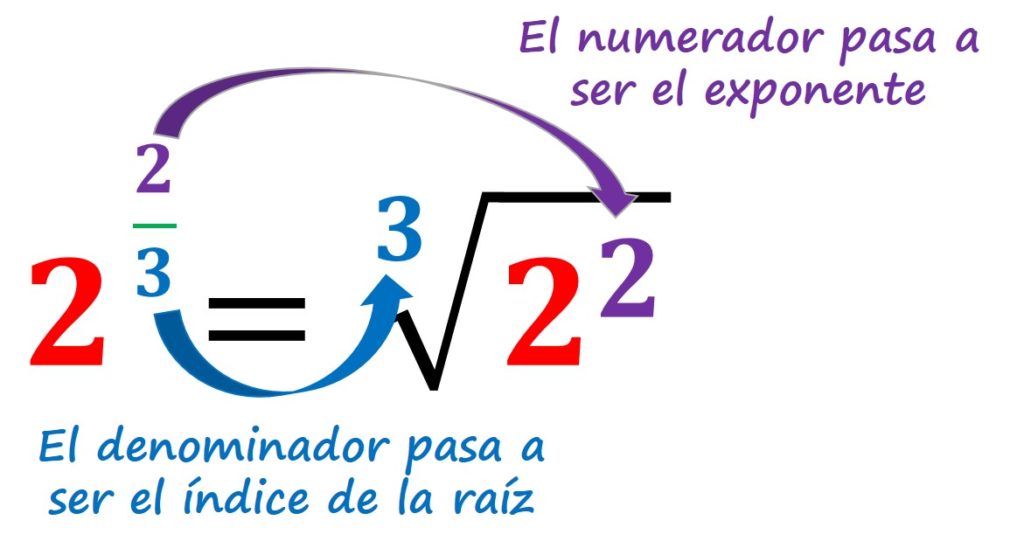
Para convertir un número o expresión con exponente fraccionario, necesitamos identificar el número y denominador del exponente. El numero pasará a ser el exponente de la base y el denominador el índice de la raíz:
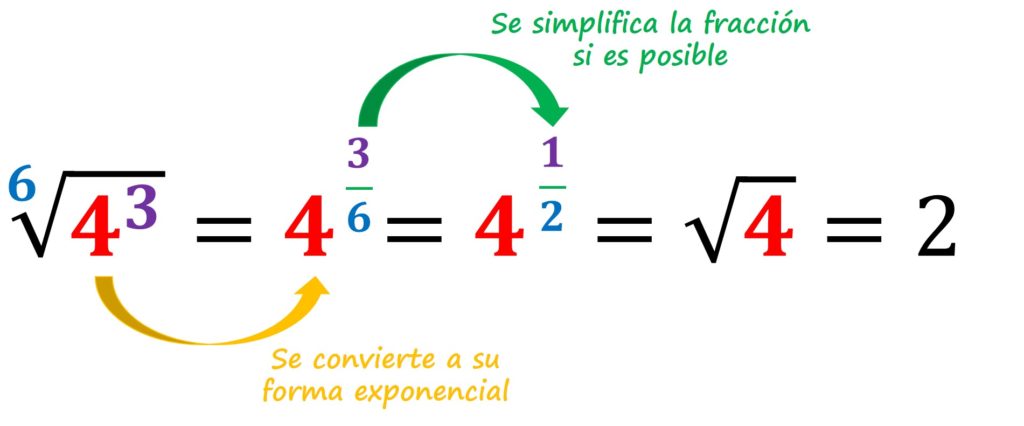
EJEMPLO 1: Resolver la siguiente expresión

SOLUCIÓN: El resolver esta expresión directamente puede llegar a ser un poco difícil, ya que tendríamos que elevar el 4 a un exponente 3 y después sacarle una raíz sexta. Como alternativa tenemos el utilizar las leyes de los exponentes para poder simplificar la expresión de la siguiente manera:
BIBLIOGRAFÍA
Ibáñez-Carrasco, P. & García-Torres, G. (2009). Matemáticas I: Aritmética y álgebra. CENGAGE Learning.
Baldor, J.A. (2004). Aritmética. Grupo Editorial Patria
