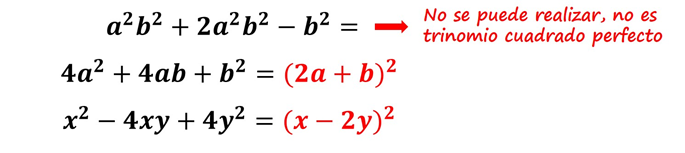6.3. TRINOMIO CUADRADO PERFECTO
Ésta es la operación inversa correspondiente al binomio al cuadrado. Una aclaración importante es que no todos los trinomios se pueden factorizar por este método. A los trinomios que pueden ser factorizados por este método se les llama trinomios cuadrados perfectos. Para que un trinomio sea cuadrado perfecto, se deben cumplir tres condiciones:
1. Debe haber tres términos.
2. Debe tener raíz cuadrada exacta el primer y el tercer término.
3. La doble multiplicación de la raíz del primer por el tercer término es el segundo término del trinomio original.

Regla de Factorización de un Trinomio Cuadrado Perfecto:
1. Se extrae la raíz cuadrada del primer y segundo término.
2. Se verifica que el doble producto de estas raíces coincida con el 2do término.
3. Se forma un binomio con las dos raíces separadas por el signo del término de en medio y se eleva al cuadrado.

Ejemplos: