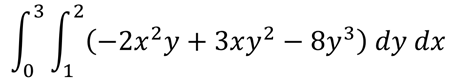7.2. INTEGRALES ITERADAS

Suele ser difícil evaluar directamente integrales a partir de su definición por medio de la suma de Riemann, pero el teorema fundamental del cálculo proporciona un método mucho más fácil. La evaluación de integrales dobles con base en los principios elementales es aún más difícil, pero aquí se verá cómo expresar una integral doble como una integral iterada, la que después puede evaluarse calculando dos integrales simples. Veámoslo con el siguiente ejemplo.

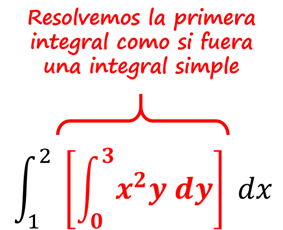
EJEMPLO 1: Evaluar la siguiente integral iterada

SOLUCIÓN: Al analizar la integral nos podemos dar cuenta que primero se debe de integrar con respecto de ‘y’ y después con respecto de ‘x’.

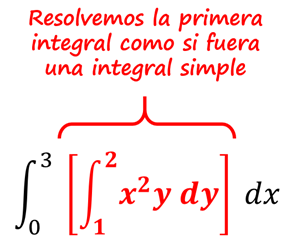
Como la primera integral es con respecto de ‘y’, entonces la ‘x’ permanece constante.

Una vez que se resuelve la integral con respecto de ‘y’ la sustituimos para posteriormente derivar con respecto de ‘x’ y obtener el resultado final.

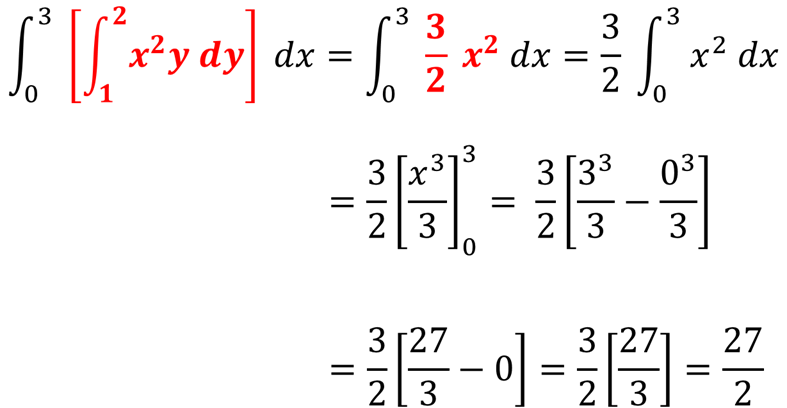
EJEMPLO 2: Evaluar la siguiente integral iterada

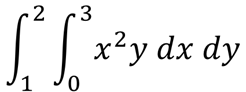
SOLUCIÓN: Como podemos observar la función es igual que la del ejemplo anterior con la diferencia que primero se debe integrar con respecto de ‘x’ y después con respecto de ‘y’.

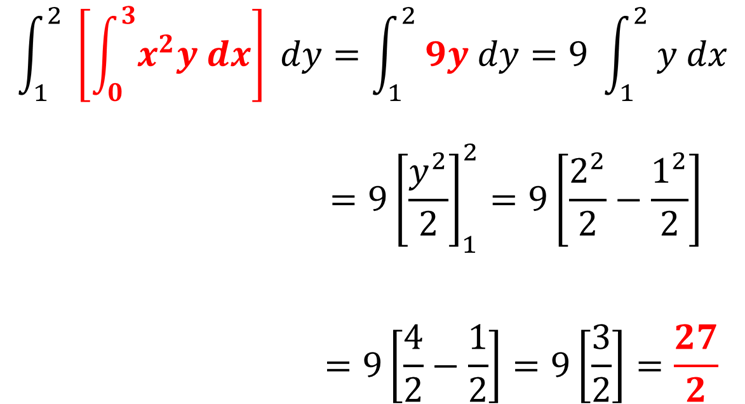
Observe que en ambos ejemplos se obtiene la misma respuesta ya sea que se integrara primero con respecto a y o x; es decir, el orden de la integración no importa.

VIDEO DE INTERÉS:

ACTIVIDAD 1: Resolver la siguiente integral iterada.